trigonométricas :jose manuel diaz diaz

     
                 Razones Trigonométricas 

Las razones trigonométricas de un ángulo α son las razones obtenidas entre los tres lados de un triángulo rectángulo. Es decir, la comparación por su cociente de sus tres lados a, b y c.

Sea α uno de los ángulos agudos del triángulo rectángulo.

• El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la hipotenusa (c).
  
• El coseno se define como la razón entre el cateto contiguo o cateto adyacente (b) y la hipotenusa (c).
  
• La tangente es la razón entre el cateto opuesto (a) y el cateto contiguo o cateto adyacente (b).
  

Razones trigonométricas de ángulos característicos

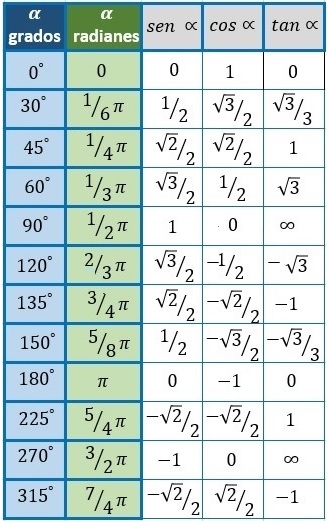
El seno, coseno y tangente de los ángulos más característicos (0º, 30º, 45º, 60º, 90º, 180º y 270º) son:

Relación entre razones trigonométricas

ANUNCIOS

Cualquier razón trigonométrica se puede expresar en función de cualquier otra. En la siguiente tabla se puede ver la fórmula con la que se expresa cada una en función de la otra.

Nota: el signo ± que corresponde en cada caso depende del cuadrante en que esté el ángulo.

Razones trigonométricas del ángulo complementario

• Seno del ángulo complementario:
  
• Coseno del ángulo complementario:
  
• Tangente del ángulo complementario:
  

Razones trigonométricas del ángulo suplementario

• Seno del ángulo suplementario:
  
• Coseno del ángulo suplementario:
  
• Tangente del ángulo suplementario:
  

Razones trigonométricas del ángulo conjugado

• Seno del ángulo conjugado:
  
• Coseno del ángulo conjugado:
  
• Tangente del ángulo conjugado:
  

Razones trigonométricas del ángulo opuesto

• Seno del ángulo opuesto:
  
• Coseno del ángulo opuesto:
  
• Tangente del ángulo opuesto:
  

Razones trigonométricas del ángulo que difiere 90º

• Seno del ángulo que difiere 90º:
  
• Coseno del ángulo que difiere 90º:
  
• Tangente del ángulo que difiere 90º:
  

Razones trigonométricas del ángulo que difiere 180º

• Seno del ángulo que difiere 180º:
  
• Coseno del ángulo que difiere 180º:
  
• Tangente del ángulo que difiere 180º:
  

Razones trigonométricas del ángulo suma

• Seno del ángulo suma:
  
• Coseno del ángulo suma:
  
• Tangente del ángulo suma:
  

Razones trigonométricas del ángulo resta

• Seno del ángulo resta:
  
• Coseno del ángulo resta:
  
• Tangente del ángulo resta:
  

Razones trigonométricas del ángulo doble

• Seno del ángulo doble:
  
• Coseno del ángulo doble:
  
• Tangente del ángulo doble:
  

Razones trigonométricas del ángulo mitad

• Seno del ángulo mitad:
  
• Coseno del ángulo mitad:
  
• Tangente del ángulo mitad:
  

Razones trigonométricas del ángulo triple

• Seno del ángulo triple:
  
• Coseno del ángulo triple:
  
• Tangente del ángulo triple:
  

Razones trigonométricas recíprocas de α

A partir de las razones del seno, coseno y tangente se pueden definir las razones inversas.

• Cosecante de α:
  
• Secante de α:
  
• Cotangente de α:
  

Funciones trigonométricas inversas

Las funciones trigonométricas inversas se definen como las inversas de las razones trigonométricas.

Son funciones trigonométricas inversas: arcoseno, arcocoseno y arcotangente.

Funciones trigonométricas

Las funciones trigonométricas se llaman también funciones circulares. El motivo es que el punto B del triángulo que se ha dibujado sobre el eje de coordenadas, con el vértice del ángulo α en el centro de una circunferencia(O), puede recorrer todos los puntos de esta última.

Se pueden representar gráficamente las razones y las razones inversasen el triángulo sobre una circunferencia de radio r=1.

Medida de ángulos

Razones trigonométricas

Razones trigonométricas de α

Fórmulas trigonométricas

Ejemplos de aplicación de estas fórmulas

Uso de la calculadora

Razones de ángulos

Razones trigonométricas
Grados	0º	90º	180º	270º	30º	45º	60º
Radianes	2π	π ⁄ 2	π	3π ⁄ 2	π ⁄ 6	π ⁄ 4	π ⁄ 3
Seno	0	1	0	-1	1 ⁄ 2	√2 ⁄ 2	√3 ⁄ 2
Coseno	1	0	-1	0	√3 ⁄ 2	√2 ⁄ 2	1 ⁄ 2
Tangente	0	∞	0	− ∞	√3 ⁄ 3	1	√3

Razones de los ángulos de 30°, 45° y 60°

si te a gustado!COMPÁRTELO!

empieza asiendo lo necesario ,después lo posible,y de repente te encontraras asiendo lo imposible

presentado a: ANDREY CASAS

POR: JOSE MANUEL DIAZ DIAZ